数据结构与算法——二叉树

二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个结点。

相关术语

• 结点：包含一个数据元素及若干个指向其子结点的信息
• 结点的权：结点中存储的数据的值
• 路径：从根结点找到该结点的路线
• 度：一个结点拥有子结点的个数被称为结点的度，一个树中，所有结点中最大的度被称为树的度
• 叶子结点（终端结点）：没有任何子结点的结点被称为叶子结点（度为0的结点）
• 分支结点（非终端结点）：度不为0的结点
• 结点的层：跟结点处于第一层，根结点的子结点处于第二层，以此类推。二叉树的结点所在的层为（log2(n)）
• 树的深度（高度）：所有结点层次最大的值
• 有序树：树中各棵子树的次序是有先后次序的树
• 无须树：树中各棵子树的次序是有先后次序的树
• 空树：没有任何结点的树
• 森林：由m（m≥0）棵互不相交的树构成一片森林。如果把一棵非空的树的根结点删除，则该树就变成了一片森林，森林中的树由原来根结点的各棵子树构成
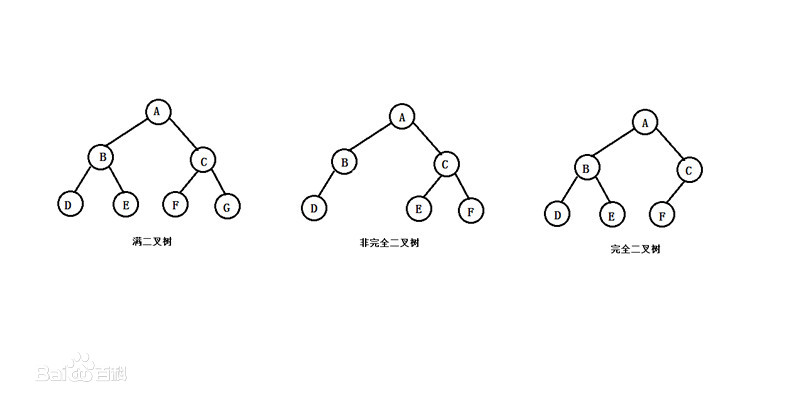
• 满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树
• 完全二叉树：深度为k，有n个结点的二叉树当且仅当其每一个结点都与深度为k的满二叉树中编号从1到n的结点一一对应时，称为完全二叉树。完全二叉树的特点是叶子结点只可能出现在层序最大的两层上，并且某个结点的左分支下子孙的最大层序与右分支下子孙的最大层序相等或大1
• 前序遍历：二叉树遍历方式的一种，从根结点开始，先操作结点值，然后操作左结点值，最后操作右结点值，递归执行。
• 中序遍历：二叉树遍历方式的一种，从根结点开始，先操作左结点值，然后操作结点值，最后操作右结点值，递归执行。
• 倒序遍历：二叉树遍历方式的一种，从根结点开始，先操作左结点值，然后操作右结点值，最后操作结点值，最递归执行。

代码示例

package BinaryTree;

public class BinaryTree {
    //根结点
    private Node root;

    /**
     * @param node
     */
    public void setRoot(Node node)
    {
        this.root = node;
    }

    /**
     * 新增节点
     *
     * @param supNode 父节点
     * @param subNode 子结点
     * @param isLeft  是否在左子结点上增加
     */
    public void add(Node supNode, Node subNode, boolean isLeft)
    {
        if (isLeft) {
            supNode.setLeft(subNode);
        } else {
            supNode.setRight(subNode);
        }
    }

    //前序遍历
    public void preTraverse()
    {
        this.preTraverse(this.root);
    }

    public void preTraverse(Node node)
    {
        //先展示当前节点的值
        System.out.printf("节点的值：%d \n", node.getValue());
        //然后展示左节点
        if (node.getLeft() != null) {
            this.preTraverse(node.getLeft());
        }
        //最后展示右节点
        if (node.getRight() != null) {
            this.preTraverse(node.getRight());
        }
    }

    //中序遍历
    public void midTraverse()
    {
        this.midTraverse(this.root);
    }

    public void midTraverse(Node node)
    {
        //先展示展示左节点
        if (node.getLeft() != null) {
            this.preTraverse(node.getLeft());
        }
        //然后当前节点的值
        System.out.printf("节点的值：%d \n", node.getValue());
        //最后展示右节点
        if (node.getRight() != null) {
            this.preTraverse(node.getRight());
        }
    }

    //后序遍历
    public void postTraverse()
    {
        this.postTraverse(this.root);
    }

    public void postTraverse(Node node)
    {
        //然后展示左节点
        if (node.getLeft() != null) {
            this.preTraverse(node.getLeft());
        }
        //先展示展示右节点
        if (node.getRight() != null) {
            this.preTraverse(node.getRight());
        }
        //最后当前节点的值
        System.out.printf("节点的值：%d \n", node.getValue());
    }
}

class Node {
    private Node left;
    private Node right;
    private int value;

    public Node(int value)
    {
        this.value = value;
    }

    public Node getLeft()
    {
        return left;
    }

    public void setLeft(Node left)
    {
        this.left = left;
    }

    public Node getRight()
    {
        return right;
    }

    public void setRight(Node right)
    {
        this.right = right;
    }

    public int getValue()
    {
        return value;
    }

    public void setValue(int value)
    {
        this.value = value;
    }
}

//代码执行
class Main {

    public static void main(String[] args)
    {
        BinaryTree binaryTree = new BinaryTree();

        //设置root节点
        Node node1 = new Node(10);
        binaryTree.setRoot(node1);

        //新增节点
        Node node2 = new Node(15);
        binaryTree.add(node1, node2, true);
        Node node3 = new Node(20);
        binaryTree.add(node1, node3, false);
        Node node4 = new Node(30);
        binaryTree.add(node2, node4, true);
        Node node5 = new Node(40);
        binaryTree.add(node2, node5, false);
        Node node6 = new Node(45);
        binaryTree.add(node3, node6, true);

        binaryTree.preTraverse();
    }
}

二叉树的顺序结构存储

从数据存储来看，数据存储方式和树的存储方式可以相互转换，即数组可以转化为树。将数组中的元素按次序存储到二叉树中，并且二叉树可以同原始数组相互转化。

二叉树的顺序结构存储的特点

• 顺序存储二叉树通常只考虑完全二叉树
• 第n个元素的左子节点为2*n+1
• 第n个元素的右子节点为2*n+2
• 第n个元素的父节点为(n-1)/2

通过这一特性，可以将顺序存储的二叉树实现前序、中序、后序遍历

代码示例

package BinaryTree;

/**
 * 二叉树的顺序结构存储 顺序存储
 */
public class ArrayBinaryTree {

    private int[] data;

    public ArrayBinaryTree(int[] data)
    {
        this.data = data;
    }

    /**
     * 前序遍历
     *
     * @return void
     **/
    public void preTraverse()
    {
        this.preTraverse(0);
    }

    private void preTraverse(int n)
    {
        if (n > this.data.length - 1) {
            return;
        }
        System.out.println(data[n]);
        this.preTraverse(2 * n + 1);
        this.preTraverse(2 * n + 2);
    }

    /**
     * 中序遍历
     *
     * @return void
     **/
    public void midTraverse()
    {
        this.midTraverse(0);
    }

    private void midTraverse(int n)
    {
        if (n > this.data.length - 1) {
            return;
        }
        this.midTraverse(2 * n + 1);
        System.out.println(data[n]);
        this.midTraverse(2 * n + 2);
    }

    /**
     * 后续遍历
     *
     * @return void
     **/
    public void postTraverse()
    {
        this.preTraverse(0);
    }

    private void postTraverse(int n)
    {
        if (n > this.data.length - 1) {
            return;
        }
        this.postTraverse(2 * n + 1);
        this.postTraverse(2 * n + 2);
        System.out.println(data[n]);
    }
}

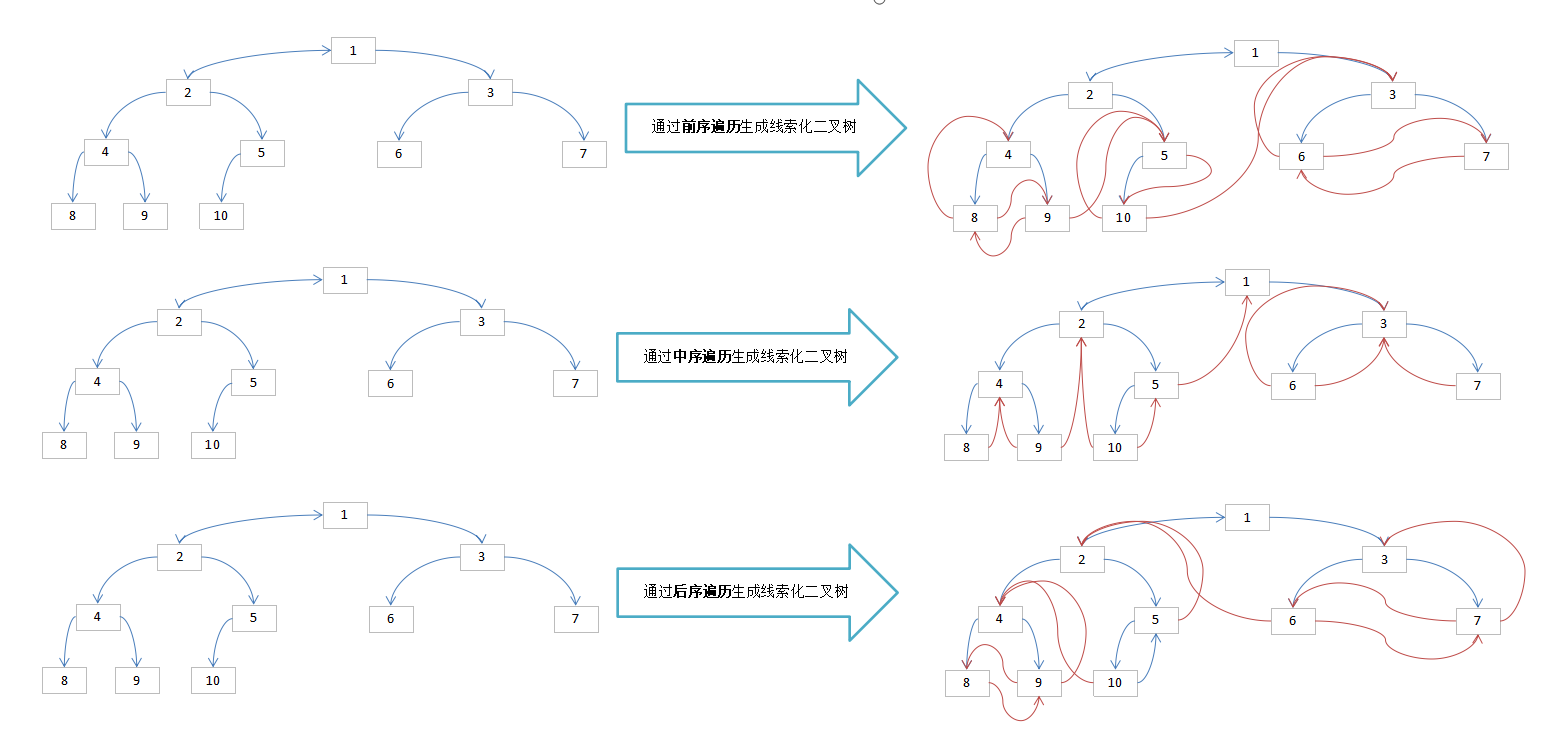
线索化二叉树

在二叉树的结点上加上线索的二叉树称为线索二叉树，对二叉树以某种遍历方式（如前序、中序、后序或层次等）进行遍历，使其变为线索二叉树的过程称为对二叉树进行线索化。

详细介绍

在二叉树中，会发现叶子结点中，通常存在两个指针为空，为了利用起它们，可以将其保存为前序|中序|后续的线索，即通过这个线索，可以快速找到上一个/下一个的结点。需要注意的点：

• 因为左右结点可以代表两种含义，所以需要定义左右结点的类型
• 因为前序/中序/后序遍历的结点的顺序不完全相同，所以前序/中序/后序的线索不通用，并且每棵树只能同时使用其中的一种方式进行线索化
• 通常来说，使用前序线索化的二叉树，对二叉树前序遍历提供方便，但对其他方式的遍历也会产生影响
• 线索化结点的左指针指向的是上一个遍历的结点，被称为“前驱结点”
• 线索化结点的右指针指向的是下一个遍历的结点，被称为“后继结点”
• 下图是前序/中序/后序二叉树线索化的示例展示

前序线索化二叉树代码

package BinaryTree;

public class ThreadBinaryTree {
    private ThreadBinaryNode root;

    public ThreadBinaryTree(ThreadBinaryNode root)
    {
        this.root = root;
    }

    //对每个叶子结点按前序创建前序线索化
    private ThreadBinaryNode prevNode;

    public void createPreThread()
    {
        if (this.root == null) {
            return;
        }
        this.createPreThread(root);
    }

    private void createPreThread(ThreadBinaryNode node)
    {
        if (node == null) {
            return;
        }

        //如果左节点为null，则需要进行线索化
        if (node.getLeft() == null) {
            //System.out.printf("设置[%d]元素的前驱结点[%d]\n", node.getValue(), this.prevNode.getValue());
            node.setLeft(this.prevNode);
            node.setLeftType(1);
        }
        //如果右节点为null，则需要线索化
        if (this.prevNode != null && this.prevNode.getRight() == null) {
            //System.out.printf("设置[%d]元素的后继结点[%d]\n", this.prevNode.getValue(), node.getValue());
            this.prevNode.setRight(node);
            this.prevNode.setRightType(1);
        }
        this.prevNode = node;

        //左节点
        if (node.getLeftType() == 0 && node.getLeft() != null) {
            this.createPreThread(node.getLeft());
        }
        //右节点
        if (node.getRightType() == 0 && node.getRight() != null) {
            this.createPreThread(node.getRight());
        }
    }

    //前序线索化二叉树的遍历
    public void preTraverse()
    {
        this.preTraverse(this.root);
    }

    private void preTraverse(ThreadBinaryNode node)
    {
        while (node != null) {
            System.out.println(node.getValue());

            if (node.getLeftType() == 0) {
                node = node.getLeft();
            } else {
                node = node.getRight();
            }
        }
    }
}

class ThreadBinaryNode {
    private ThreadBinaryNode left;
    private ThreadBinaryNode right;
    private int value;
    //0-表示结点指向 1-表示线索
    private int leftType = 0;
    private int rightType = 0;

    public ThreadBinaryNode(int value)
    {
        this.value = value;
    }

    public ThreadBinaryNode getLeft()
    {
        return left;
    }

    public void setLeft(ThreadBinaryNode left)
    {
        this.left = left;
    }

    public ThreadBinaryNode getRight()
    {
        return right;
    }

    public void setRight(ThreadBinaryNode right)
    {
        this.right = right;
    }

    public int getValue()
    {
        return value;
    }

    public void setValue(int value)
    {
        this.value = value;
    }

    public int getLeftType()
    {
        return leftType;
    }

    public void setLeftType(int leftType)
    {
        this.leftType = leftType;
    }

    public int getRightType()
    {
        return rightType;
    }

    public void setRightType(int rightType)
    {
        this.rightType = rightType;
    }
}

说明

经过线索化的二叉树通常来说，遍历起来都会非常方便，例如上述案例中，前序遍历时，不需要使用递归的方式就可以了。